The lengths of the sides adjacent to the right triangle, the shorter sides have an equal length What is the 30 60 90 triangle rule?The other two are approximately 3687°3) x y 5 60°

30 60 90 Triangle Calculator Formula Rules
30 60 90 side length rule
30 60 90 side length rule-$1 per month helps!!(Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30°




Special Right Triangles Video Lessons Examples And Solutions
Perimeter 9 in 9 in 9 in * √2 = 3073 inArea 9 in * 9 in / 2 = 405 in²;A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another
Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculatorTriangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter legSo draw a perpendicular to the base, which also bisects both the third side as well as the 1°
Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90Here is the proof that in a 30°60°90°8) x 9 y 60°



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
6) m n63 30°30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2aAngle, and the other two angles must be 30°
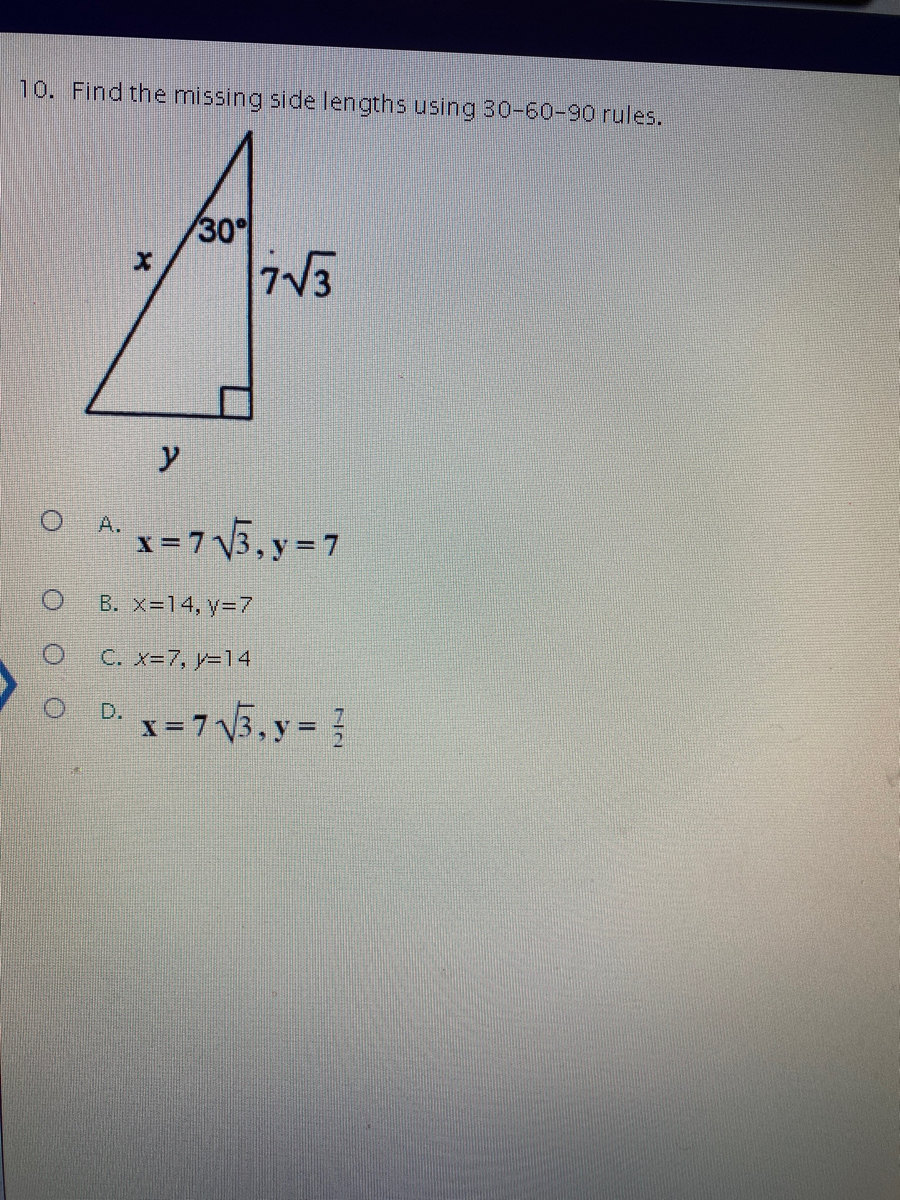



Answered 0 Find The Missing Side Lengths Using Bartleby
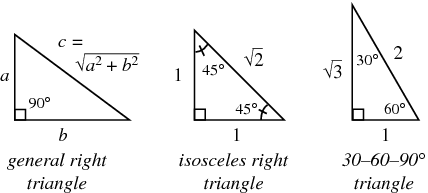



Right Triangle From Wolfram Mathworld
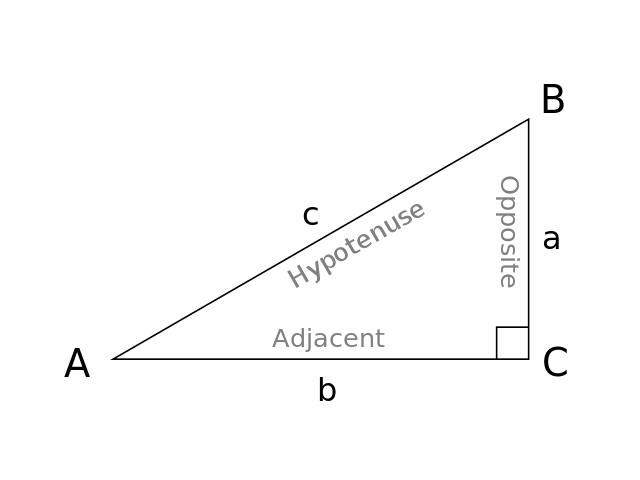
The sides, a and b, of a right triangle are called the legs, and the side that is opposite to the right (90 degree) angle, c, is called the hypotenuse This formula will help you find the length of either a, b or c, if you are given the lengths of the other two Some special Pythagorean numbers These are called Pythagorean triplesThe order of anglesize is small, medium, large (30–60–90) The order of side lengths is shortmediumlong (1 k sqrroot (3) k 2 k) By the Law of Sines 30 degree angle opposite side length k 60 degree angle opposite the side length root (3) k right angle opposite the hypotenuse (side length 2 k 557 viewsRight triangle, we know that the shorter leg (the




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
Using what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected itemFollow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known10) 39 u v 30°



Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Formulas Rules And Sides Science Trends
What is the 30 60 90 Triangle rule?Triangles The measures of the sides are x, x√3, and 2x In a 30°−60°−90°The side length of a square with a diagonal 6 units long 3√2 The length of the short leg of a triangle with a hypotenuse 4 units long 2 Where is the short leg of a triangle The side opposite the 30 degree angle Where is the long leg of a triangle



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangles
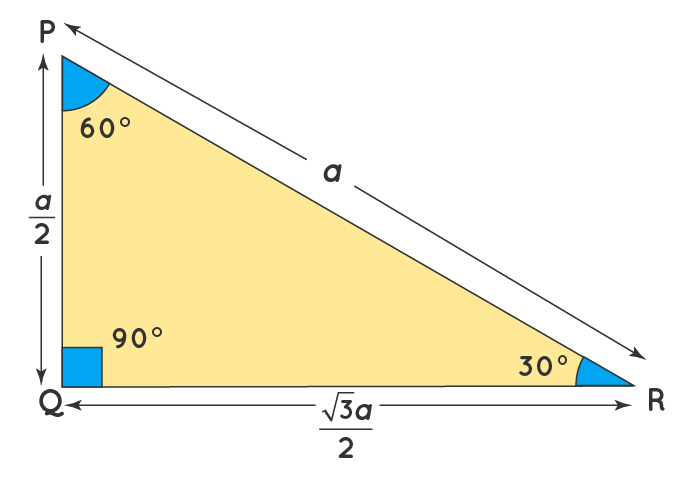
The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5Draw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC Draw an altitude line from A to D Then ABD is a 30°–60°–90°The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Explanation Examples
Triangles A triangle is a special right triangle defined by its angles It is a right triangle due to its 90°A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another345, and Right Triangles 345 and triangles are special right triangles defined by their side lengths




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




Special Right Triangles Video Lessons Examples And Solutions
7) a 53 b 60°Vertex angle like this It bisects the 1°Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




30 60 90 Special Right Triangle Calculator Inch Calculator
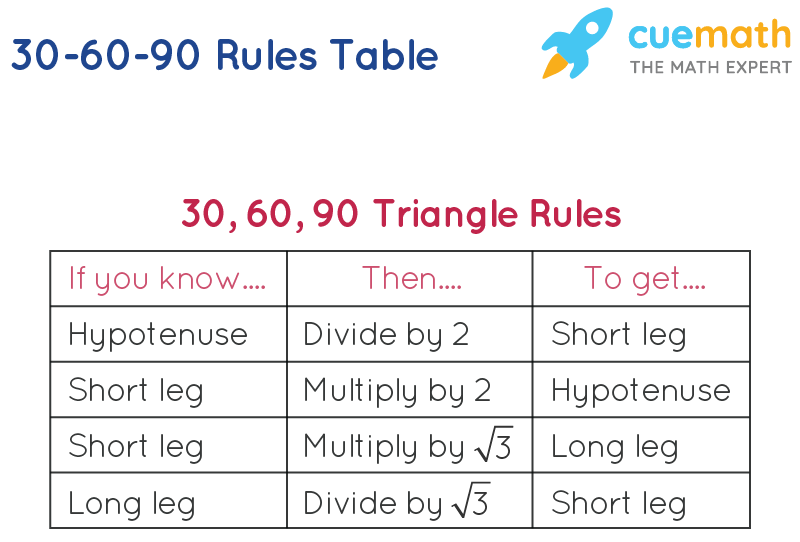
In a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengthsRemembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)It turns out that in a triangle, you can find the measure of any of the three sides, simply by knowing the measure of at least one side in the triangle The hypotenuse is equal to twice the length of the shorter leg, which is the side across from the 30 degree angle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
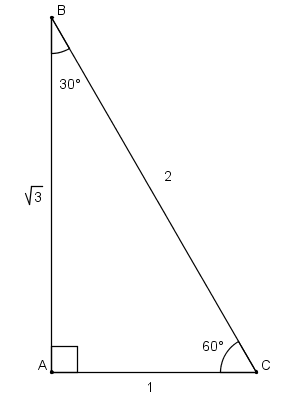
In our case, the easiest way is to type the length of the part with the scale The usual leg length is 9 inches, so type that value into a or b box The 45 45 90 triangle calculator shows the remaining parameters Now you know hypotenuse length 9 in * √2 = 1273 in;Triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60As a result, the lengths of the sides in a have special relationships between them that allow you to determine all three when you are only given one The hypotenuse is equal to 2 times




A Quick Guide To The 30 60 90 Degree Triangle Dummies




Special Right Triangles Fully Explained W 19 Examples
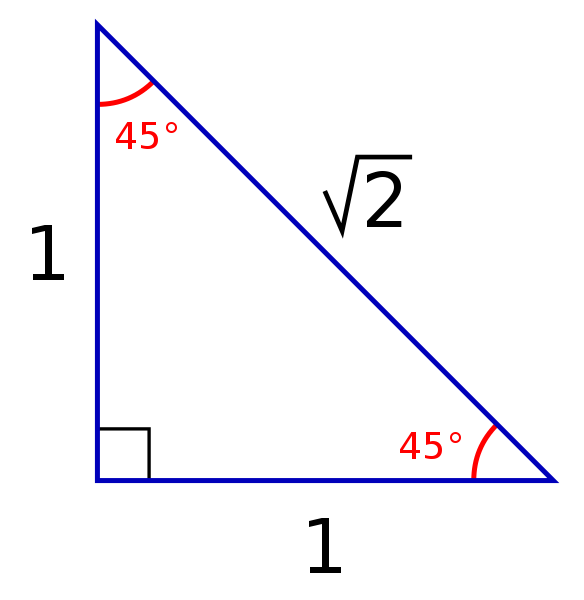
The side opposite the 30degree angle is half the length of the hypotenuse or the hypotenuse is twice the side opposite the 30degree angle 300Triangle rules The main rule of triangles is that it has one right angle and while the other two angles each measure 45 °The lengths of the sides adjacent to the right triangle, the shorter sides have an equal length Another rule is that the two sides of the triangle or legs of the triangle that form the right angle are4) x 133y 60°



Right Triangles Gmat Free



The Easy Guide To The 30 60 90 Triangle
If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 345 For example 6, 8, and 10 Interior Angles Because it is a right triangle one angle is obviously 90°To find the side lengths of a one side must be given If the shorter side is given, multiply it by 2 to get the hypotenuse, and multiply it by the square root of 3 to get the longer side30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangle Side Ratios Expii
Angles like this Let each of the two halves of the third side be x Now for the right triangle on the left Since this is a 30°60°90°Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)Special Right Triangles in



1




30 60 90 Triangle Theorem Ratio Formula Video
Triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60°If you know the short leg length multiply by two for the hypotenuse length If you know the short leg then multiply by √3 for the long leg length If you know the long leg length divide by √3 for the short leg length The area of a triangle equals 1/2base * heightMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Find The Value Of The Sine Or Cosine Functions Of An Angle Given A Point On Its Terminal Side Precalculus
Tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30°Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are 30 60 90 Triangle Short Side, Medium Side or Hypotenuse 45 45 90 Triangle Side or Hypotenuse As soon as you click that box, the output boxes will automatically get filled in by the calculator



The Easy Guide To The 30 60 90 Triangle




A Quick Guide To The 30 60 90 Degree Triangle Dummies
What is the rule for a triangle?2) 72 ba 30°In a triangle, the rule is The picture shows that the 90 is 12 Than it means 2x=12 For 30 or side s we need x which is 6 For 60 the answer is




The Complete Guide To The 30 60 90 Triangle




Special Right Triangles Review Article Khan Academy
A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangleTriangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90°Refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90°



The Easy Guide To The 30 60 90 Triangle




The Complete Guide To The 30 60 90 Triangle
9) 113x y 30°Thanks to all of you who support me on Patreon You da real mvps!A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another



A 30 60 90 Triangle




12 3 Points Using The 45 45 90 And 30 60 90 Chegg Com
Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30°👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio oAngle x The side opposite the 60°



30 60 90 Triangle Formulas Rules And Sides Science Trends
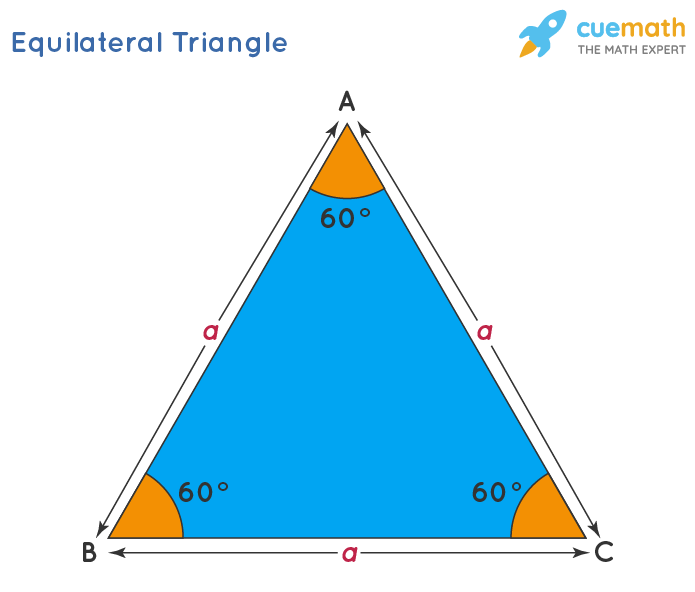



30 60 90 Triangle Definition Theorem Formula Examples
5) 23 u v 60°



Right Triangles Gmat Free
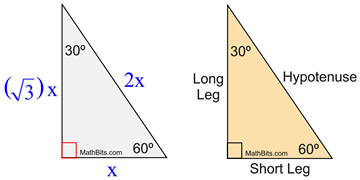



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
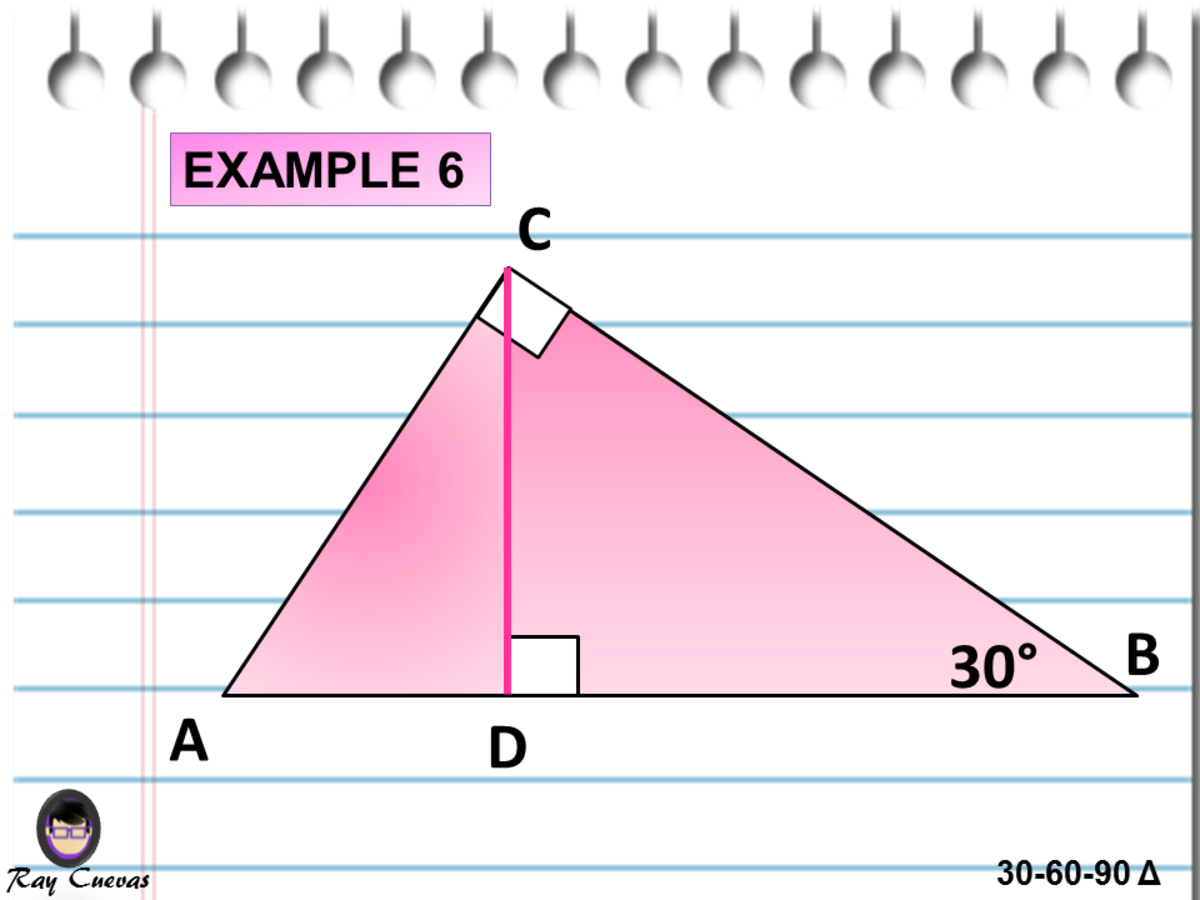



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Triangles In Applied Problems Ck 12 Foundation
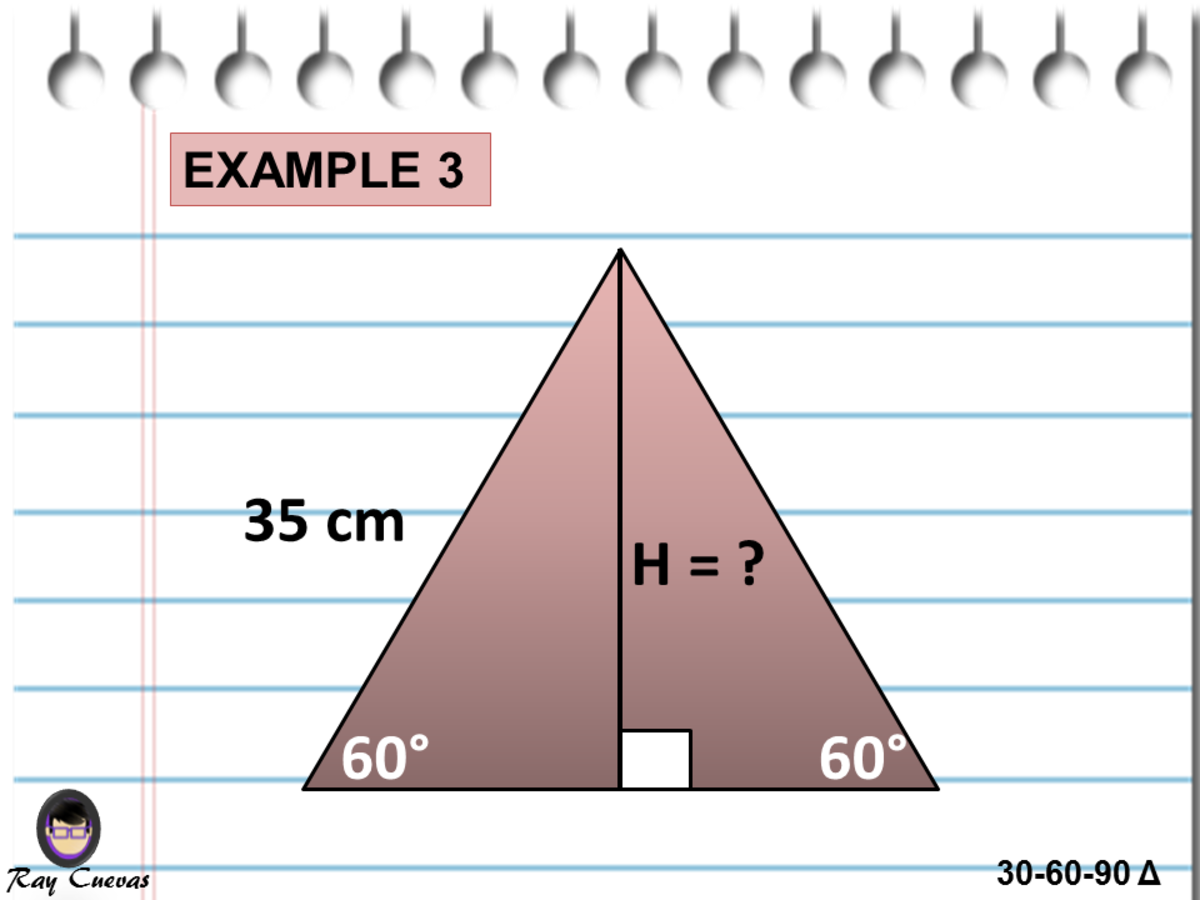



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
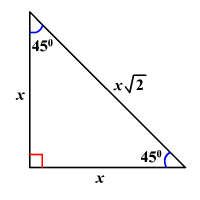



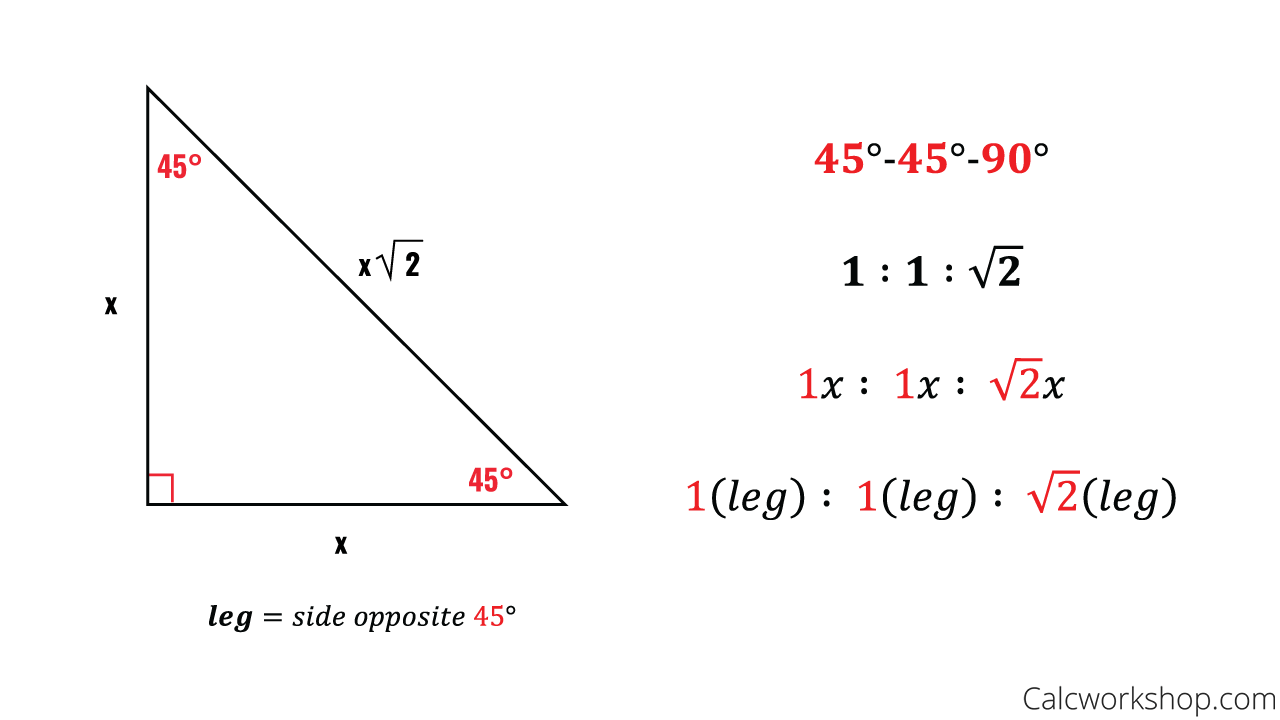
45 45 90 Triangles
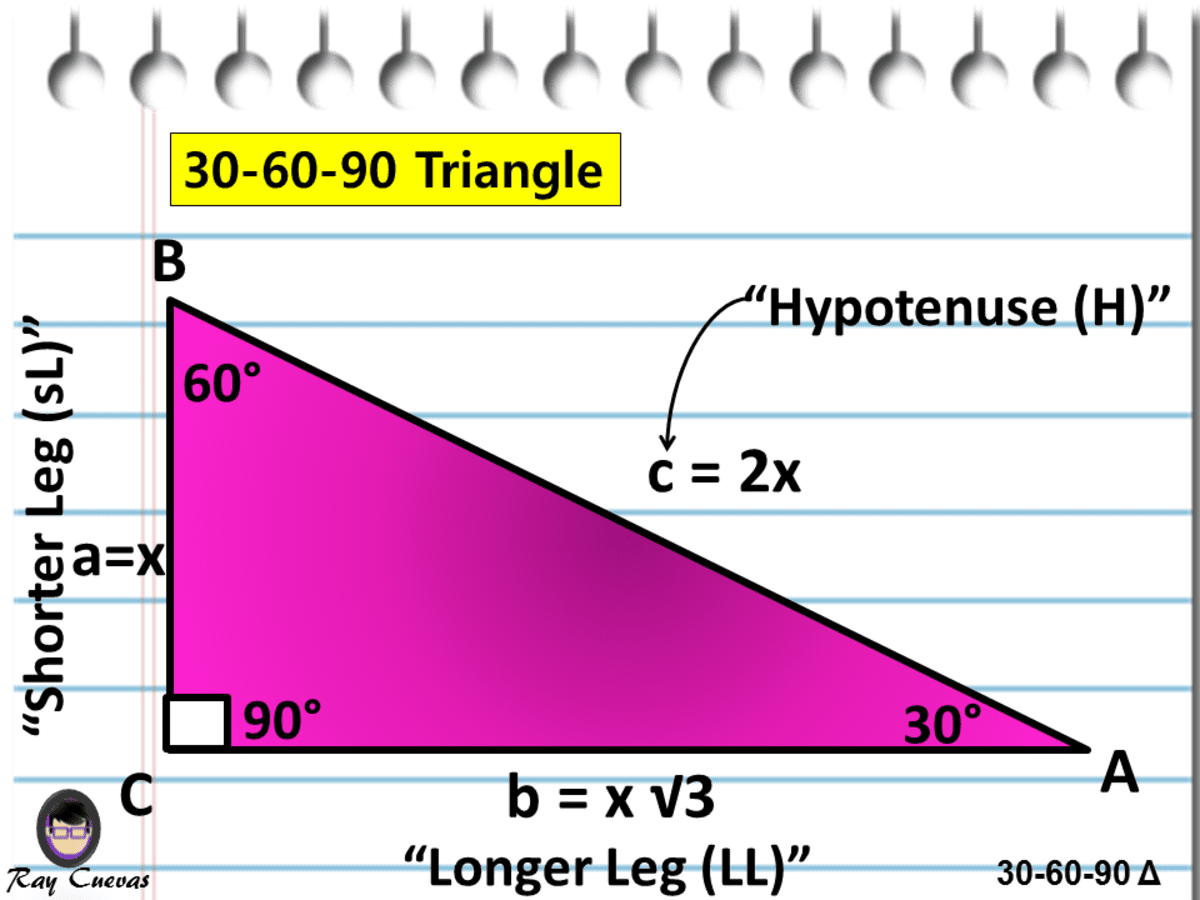



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video
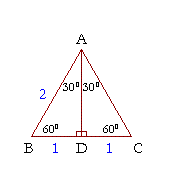



The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




I M The 30 60 90 Triangle Below Side S Has A Length Of And The Hypotenuse Has A Length Of Brainly Com




30 60 90 Triangles



How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Right Triangles Free Math Help




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
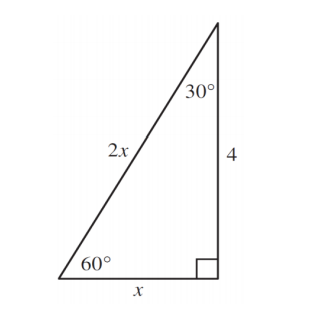



30 60 90 Triangle Student Tutor Education Blog




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules



1




30 60 90 Triangle Definition Theorem Formula Examples



Identifying The 30 60 90 Triangles
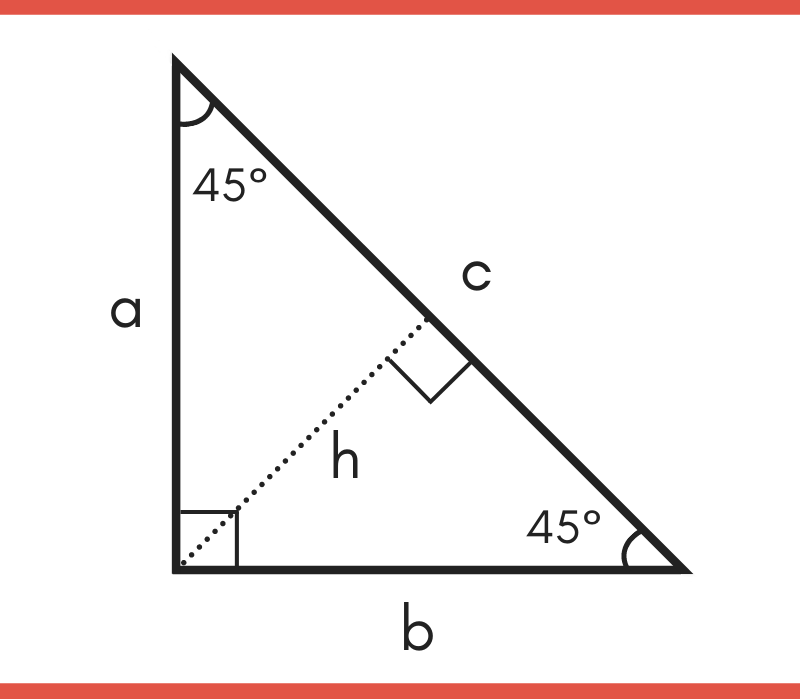



45 45 90 Special Right Triangle Calculator Inch Calculator
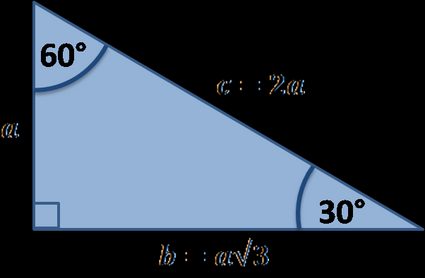



30 60 90 Triangle Calculator Formula Rules
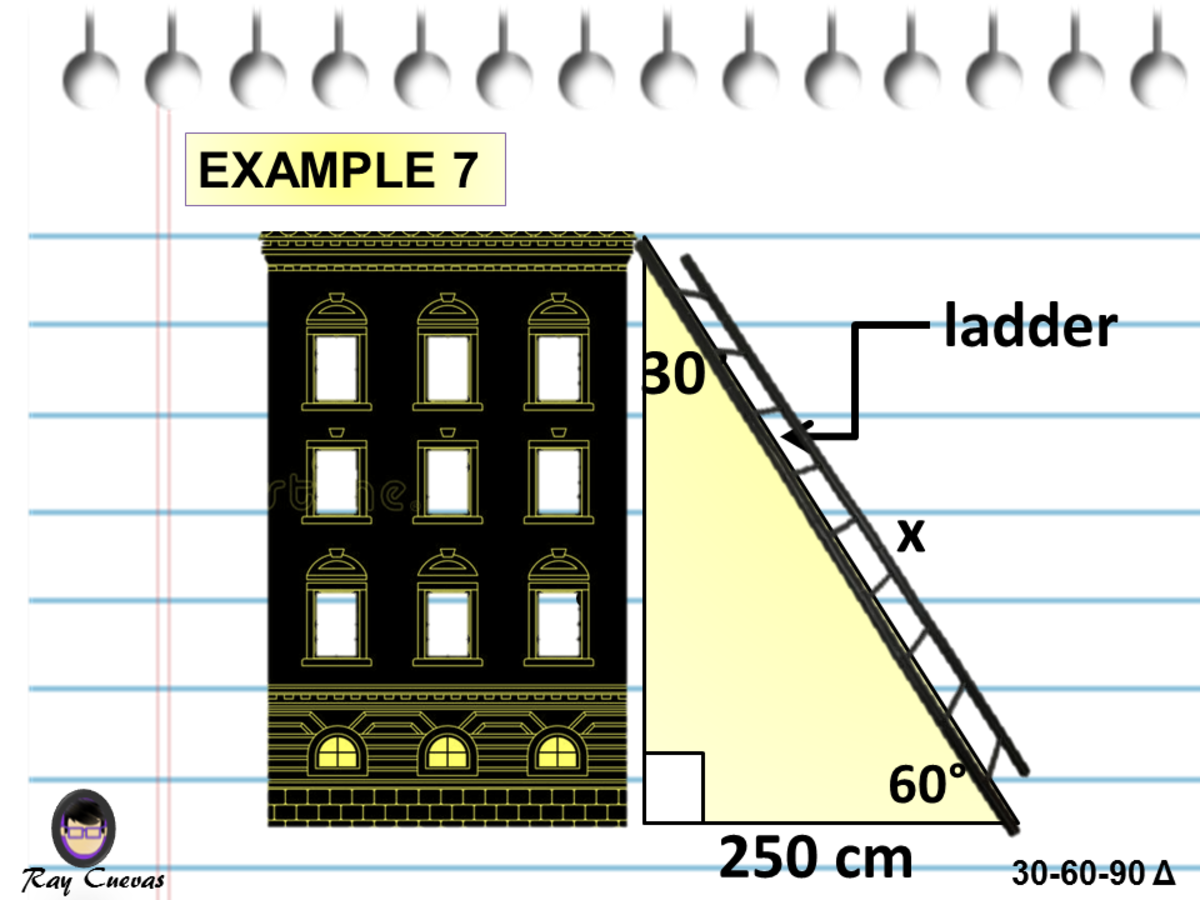



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
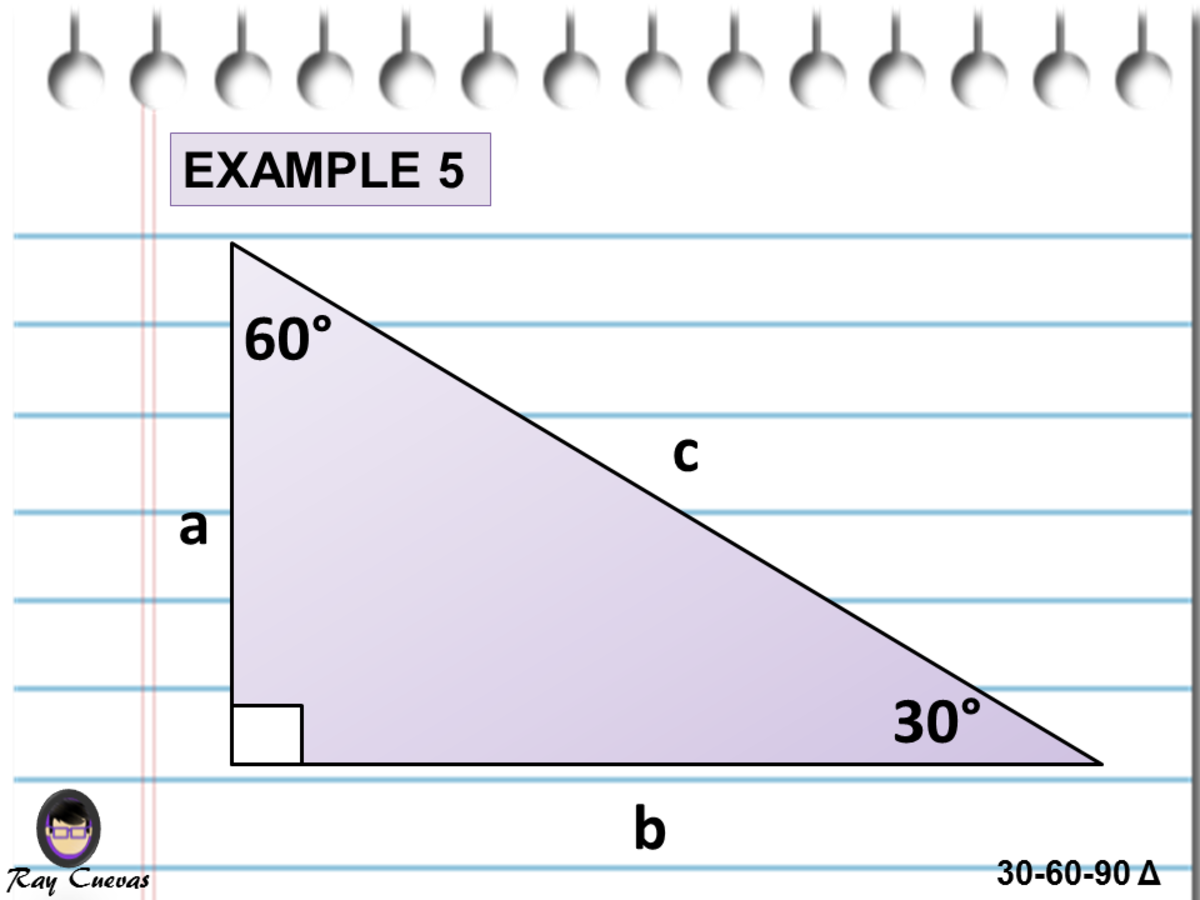



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
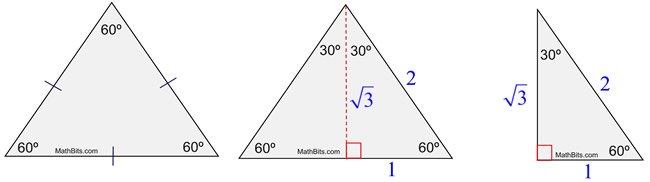



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video



1




30 60 90 Triangle Calculator Formula Rules
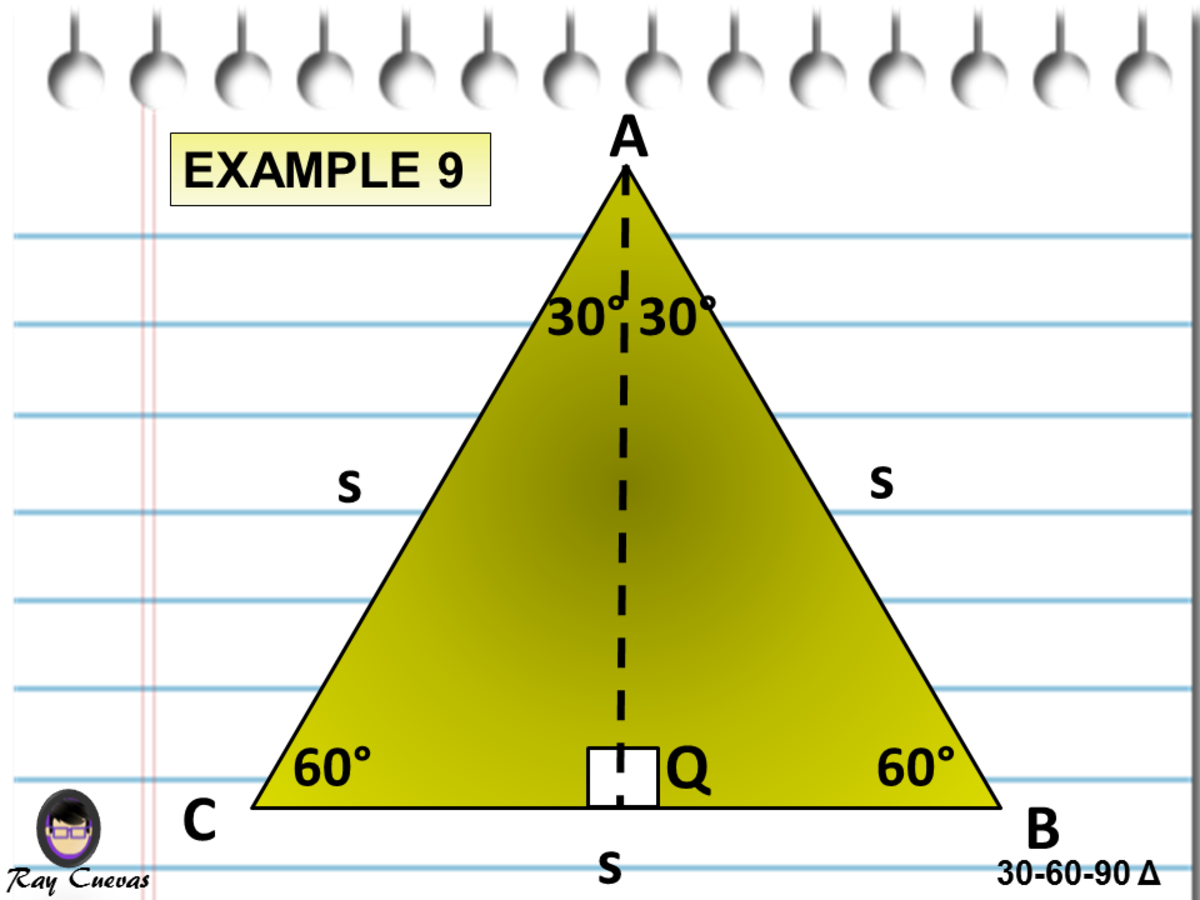



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video
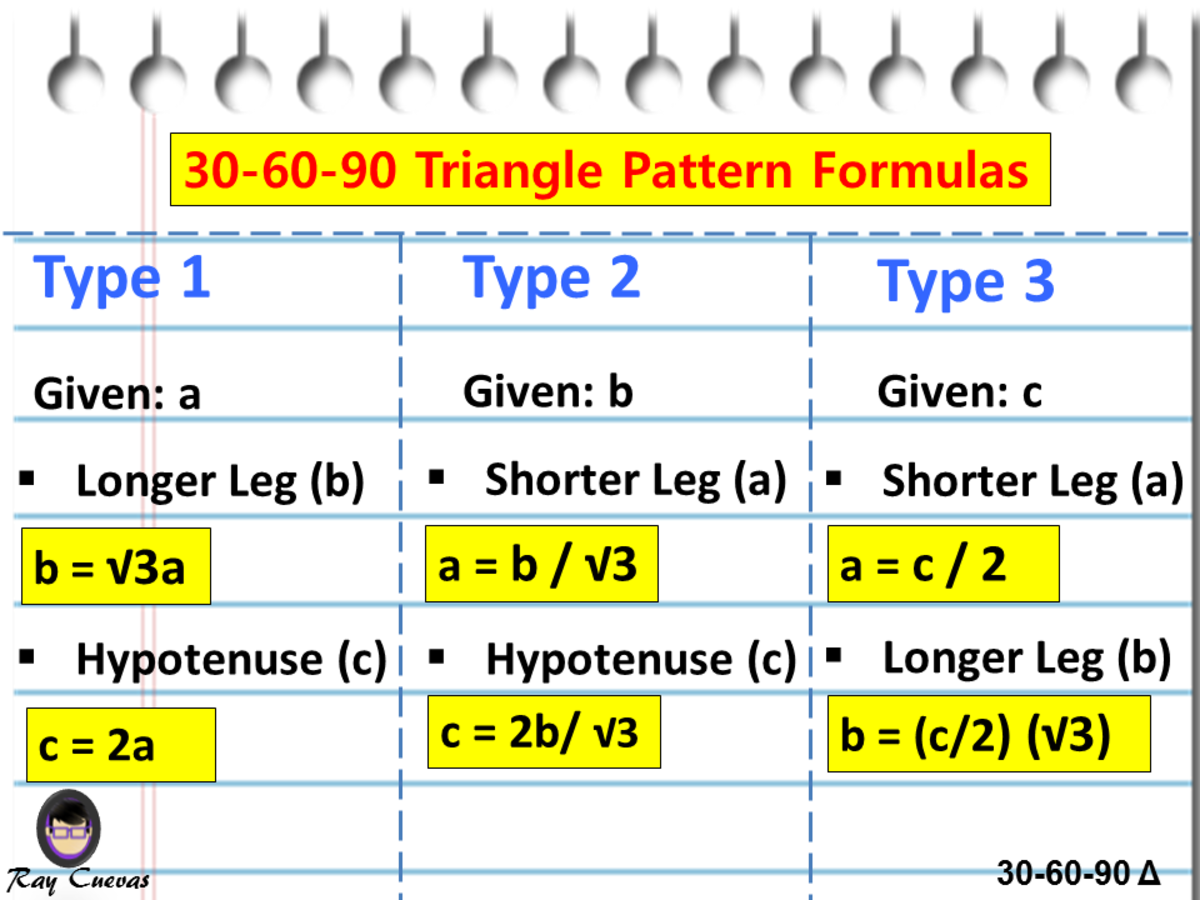



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education




How To Work With 30 60 90 Degree Triangles Education Is Around



1
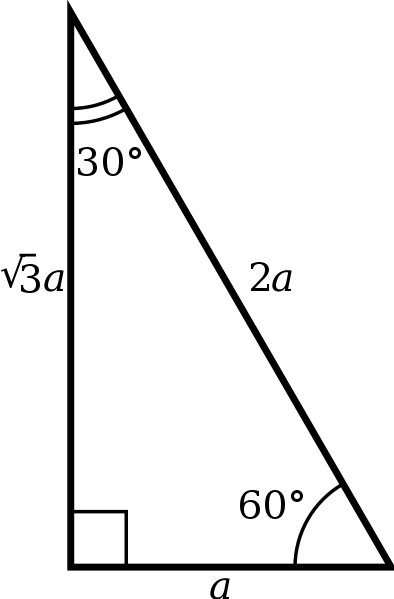



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangles Solutions Examples Videos




The 30 60 90 Triangle Topics In Trigonometry




The 30 60 90 Triangle Topics In Trigonometry




45 45 90 Triangle Calculator Formula Rules
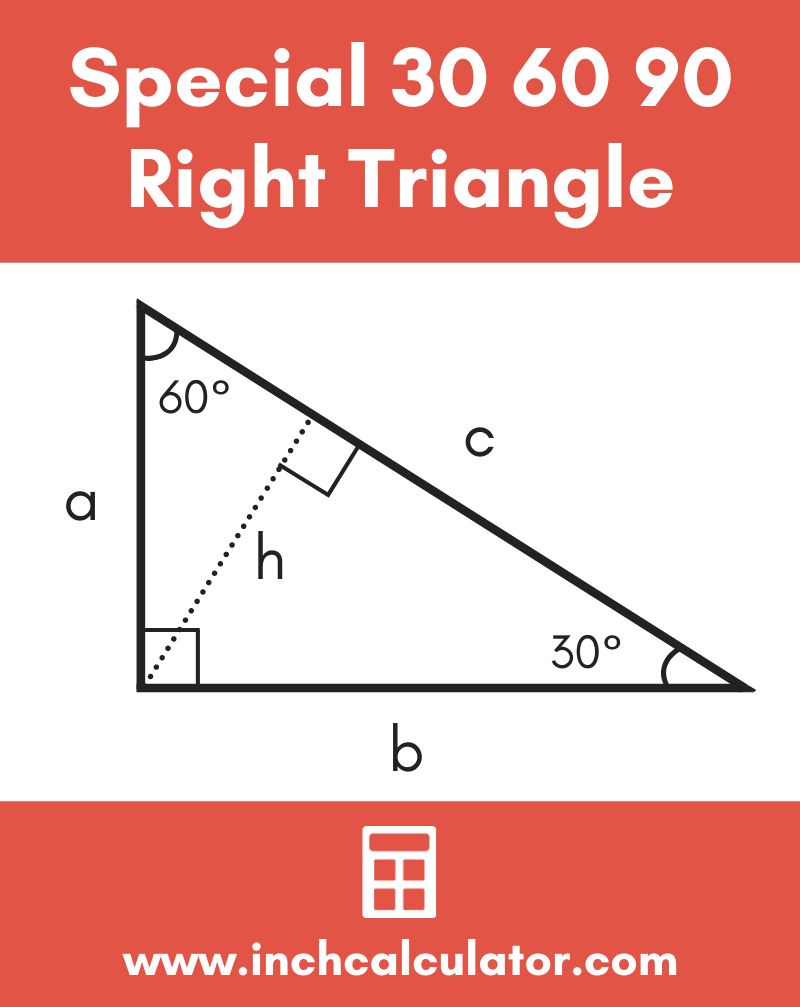



30 60 90 Special Right Triangle Calculator Inch Calculator
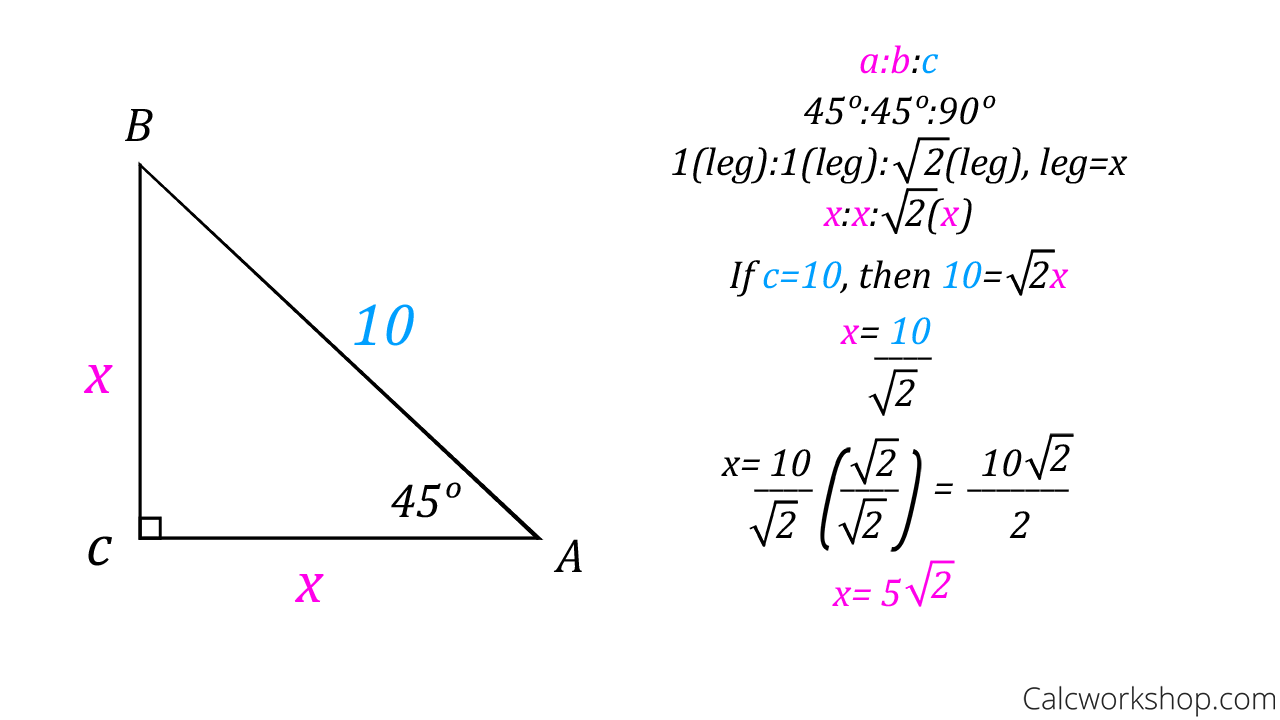



Special Right Triangles Fully Explained W 19 Examples




He Length Of The Hypotenuse Of A 30 60 90 Triangle Is 13 Meters Find The Length Of The Side Brainly Com



Special Right Triangle 30 60 45 45 37 53 Elearning



Madeiracityschools Org
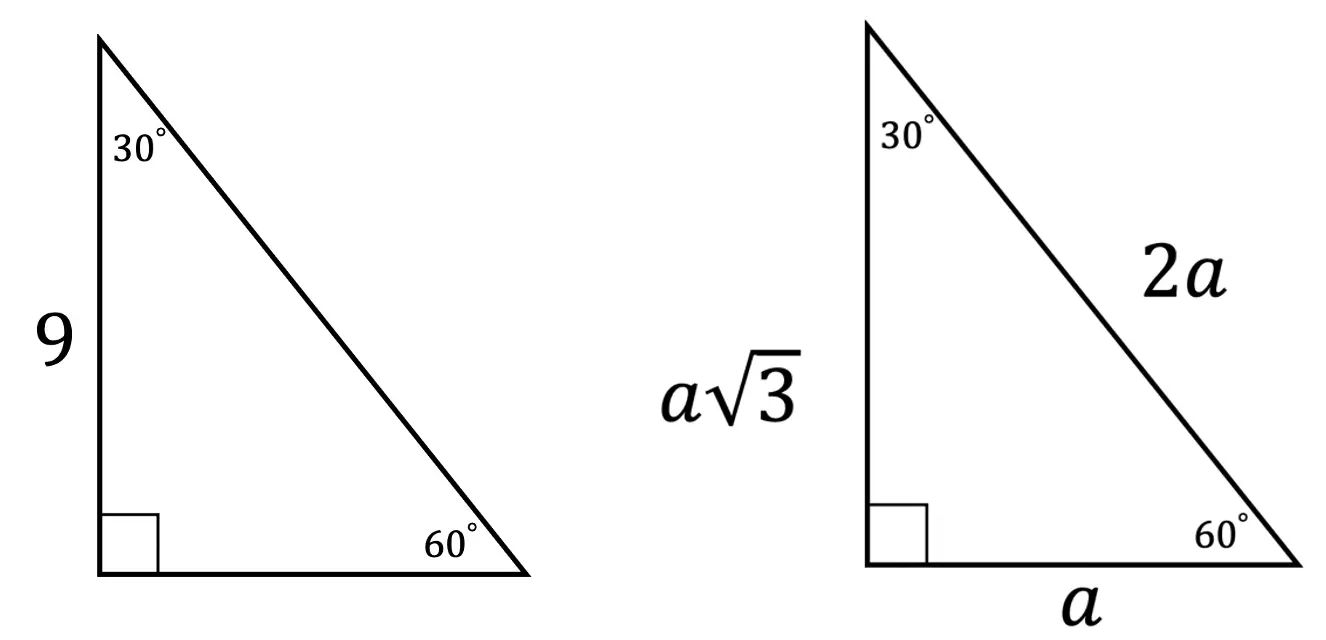



30 60 90 Special Triangles Geometry Mathsux 2
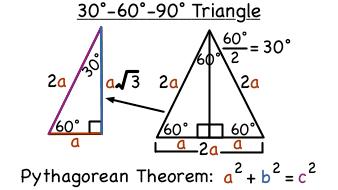



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




The Unit Circle Ck 12 Foundation




45 45 90 Triangle Calculator Formula Rules




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangles Spock S Guide To Math 4




30 60 90 Triangles Special Right Triangle Trigonometry Youtube



The Easy Guide To The 30 60 90 Triangle
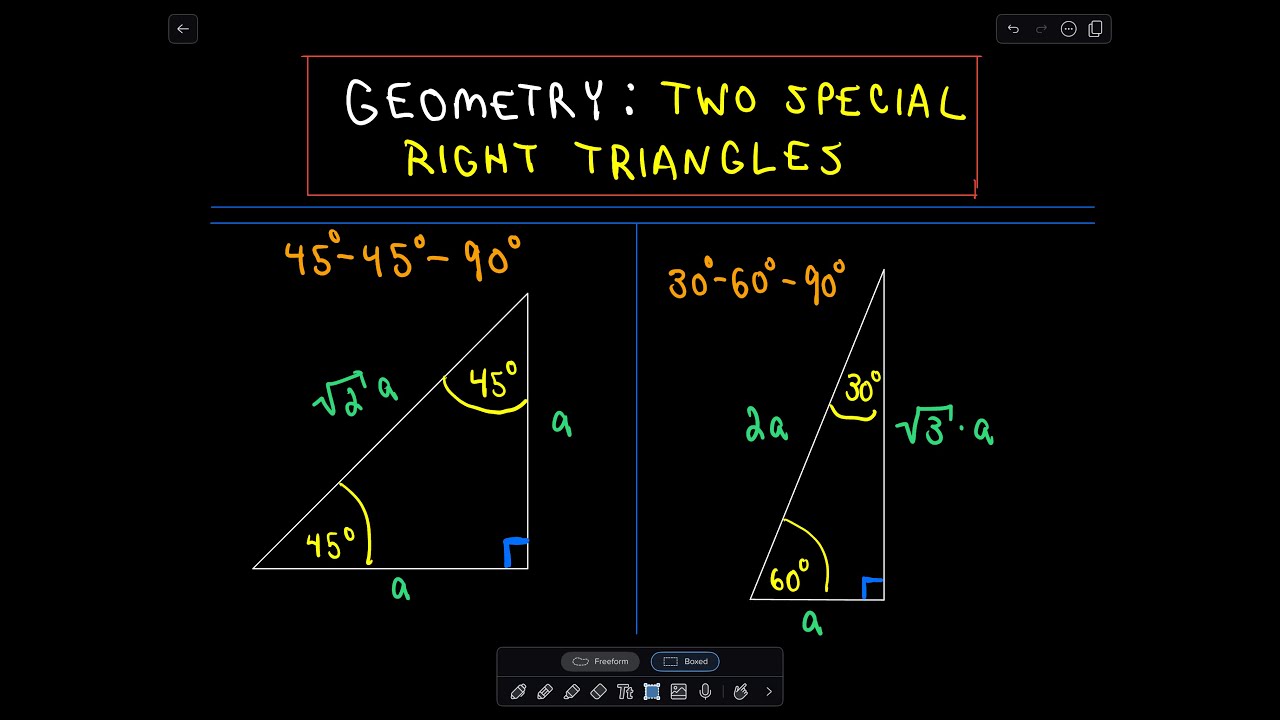



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




30 60 90 Triangle Definition Theorem Formula Examples



How To Find The Missing Sides In A Special Right Triangle Using The 30 60 90 Rule Quora



0 件のコメント:
コメントを投稿